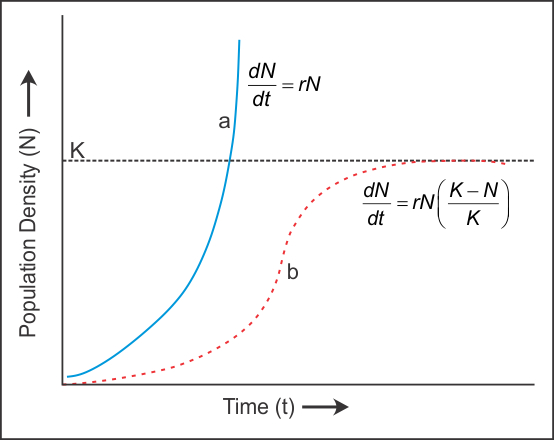
If reproduction takes place more or less continuously then this growth rate is. The expression K N is indicative of how many individuals may be added to a population at a given stage and K N divided by K is the fraction of the carrying capacity available for further growth.
Explain Verhlust Pearl Logistic Growth Of A Population With Suitable Graphical Representation Why Do Cattle Avoid Browsing On Calotropis Plants Explai Biology Topperlearning Com 1zho2ccc
51 Though the logistic has been more studied it is the Gompertz growth function that is described as being better to meet the features of some growth processes.

. Role of Intraspecific Competition. Check out the article by J. Logistic growth is a type of growth where the effect of limiting upper bound is a curve that grows exponentially at first and then slows down and hardly grows at all.
This curve describes logistic growth. Using BW data from hatch to 22 wk 3 nonlinear mathematical functions Richards Gompertz and logistic were used to estimate growth patterns of the pearl gray guinea fowl. This study was undertaken to describe the growth pattern of the pearl gray Guinea fowl.
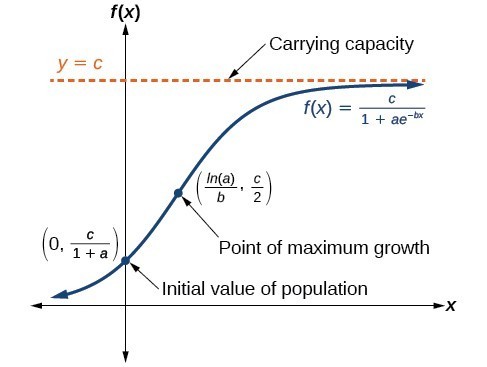
Theoretically there are several important features of the logistic growth model. A function that models the exponential growth of a population but also considers factors like the carrying capacity of land and so on is called the logistic function. Logistic Growth Model Part 1.
In logistic growth a population will continue to grow until it reaches carrying capacity which is the maximum number of individuals the environment can support. The logistic and Gompertz models are a special case of the Richards model which has a variable point of. Describe the shape of the curve and give the name of this shape.
The logistic growth causes relatively constant growth rate in the population. If a population grows from a very low level following the logistic growth model describe the main features of what a plot of the population level should look like as a function of time. In logistic growth population expansion decreases as resources become scarce and it levels off when the carrying capacity of the environment is reached resulting in an.
The logistic growth curve is S-shaped. If a population is growing in a constrained environment with carrying capacity K and absent constraint would grow exponentially with growth rate r then the population behavior can be described by the logistic growth model. Logistic growth produces an S-shaped curve.
A new pharmacodynamic model for the analysis of in vitro bactericidal kinetics was developed based on the logistic growth model with the bacterial phases divided into two compartments. Log phase lag phase deceleration phase and stationary phase. A biological population with plenty of food space to grow and no threat from predators tends to grow at a rate that is proportional to the population-- that is in each unit of time a certain percentage of the individuals produce new individuals.
The formula we use to calculate logistic growth adds the carrying capacity as a moderating force in the growth rate. In logistic growth population expansion decreases as resources become scarce and it levels off when the carrying capacity of the environment is reached. The exponential growth causes an explosion of the population.
If growth is limited by resources such as food the exponential growth of the population begins to slow as competition for those resources increases. When resources are limited populations exhibit logistic growth. Vandermeer 2010 for a more detailed explanation of the equations that describe exponential and logistic growth.
The geometric or exponential growth of all populations is eventually curtailed by food availability competition for other resources predation disease or some other ecological factor. 13 to describe the growth of animals. If a population grows from a very low level following the logistic growth model describe the main features of what a plot of the population level should look like as.
P n P n1 r1 P n1 KP n1 P n P n 1 r 1 P n 1 K P n 1. The model equations are expressed as nonlinear simultaneous differential equations and the Runge-Kutta-Gill metho. The three key features of the logistic growth are.
Exponential growth produces a J-shaped curve. Richards growth curve was used for fitting experimental data by Nelder 14 who used the term generalized logistic equation to describe the equation. Describe the shape of the curve and give the name of this shape.
The logistic growth curve is S-shaped. Like the logistic growth equation it increases monotonically with both upper and lower asymptotes. The logistic curve will continue up to certain level called the level of.
Its represented by the equation. In logistic growth population expansion decreases as resources become scarce and it levels off when the carrying capacity of the environment is reached. In exponential growth curve the rate of growth of y per unit of time is directly proportional to y but in practice the rate of growth cannot be in the same proportion always.
Logistic Growth is characterized by increasing growth in the beginning period but a decreasing growth at a later stage as you get closer to a maximum. When resources are limited populations exhibit b logistic growth. Logistic growth is similar to exponential growth except that it assumes an essential sustainable maximum point.
For example in the Coronavirus case this maximum limit would be the total number of people in the world because when everybody is sick the growth will necessarily diminish. The logistic growth has four phases. Logistic growth takes place when a populations per capita growth rate decreases as population size approaches a maximum imposed by limited resources the carrying capacity.
Although life histories describe the way many characteristics of a population. 1 the sand transport rate fx ultimately approaches the maximum capacity fmax 2 the relative growth rate dfx fxdx declines linearly with increasing fx and 3 fx at the inflection point where the growth rate dfxdx is a maximum is exactly equal to fmax2. In logistic growth population expansion decreases as resources become scarce and it levels off when the carrying capacity of the environment is reached resulting in an S-shaped curve.
Use Logistic Growth Models College Algebra

0 Comments